Matlab Coding
输出
fprintf('...'):输出字符;
提取数组、矩阵中元素
1
$ a = A(1); b = B(:,1)
矩阵运算:点乘、逆、转置、行列式
1
2
3
4
$ ans = dot(a,b)
$ ans = inv(T)
$ ans = T'
$ ans = det(T)
绘图
plot(x[,y][,'r']):直接绘制图像;subplot(221): 子窗口绘制图像;title('helloworld'): 设置标题;legend('1','2','3'): 按绘制顺序给图像标注;axis equal; axis([0 5 0 5]): 设置轴刻度范围figure('NumberTitle', 'off', 'Name', 'abc'):隐藏标题号码,设置标题;
其他
tic, ...(执行程序), toc:计算程序执行时间;edit file.m:打开文件;
2DPose
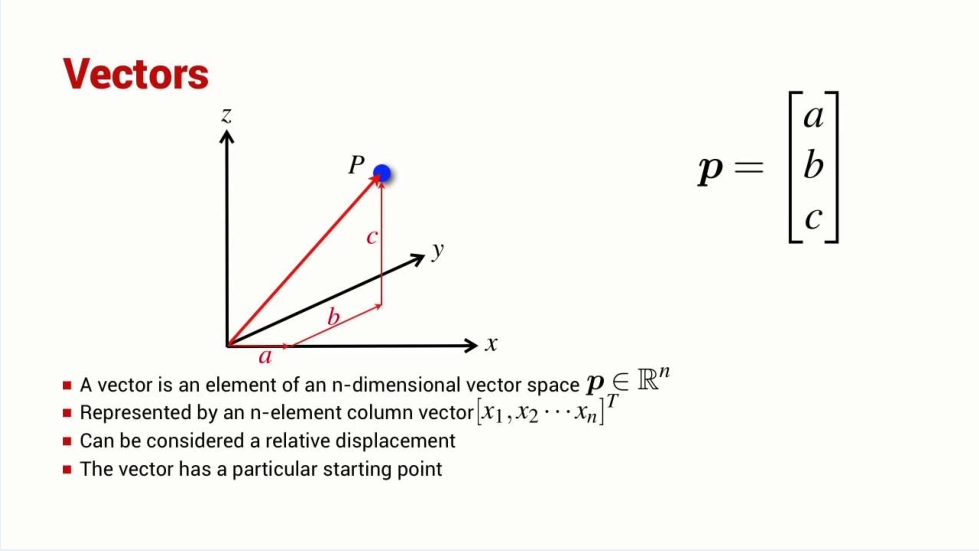
Positon and Pose
- How to describe a point and pose?
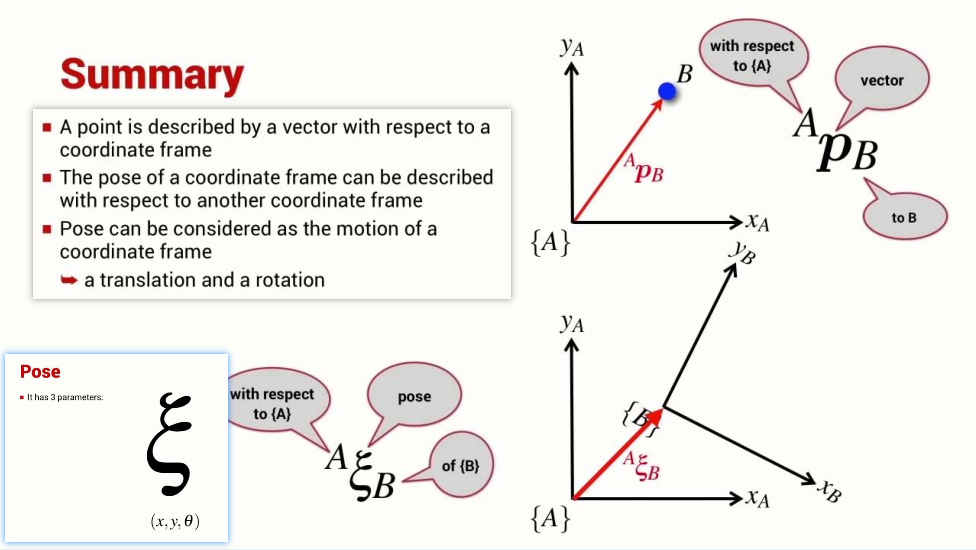
Relative Positions
- How to transform vector from one frame to another?
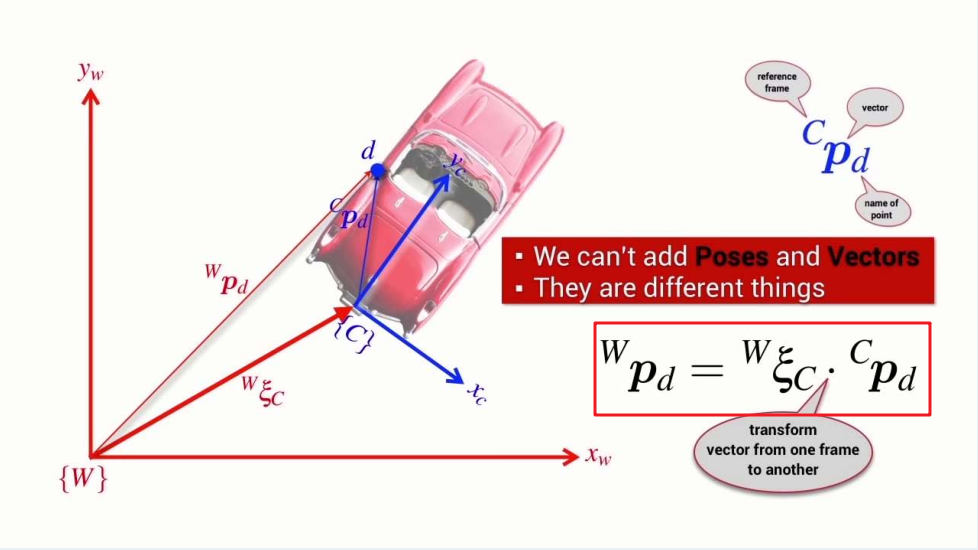
Relative Poses
How to calculate the relative points or poses?
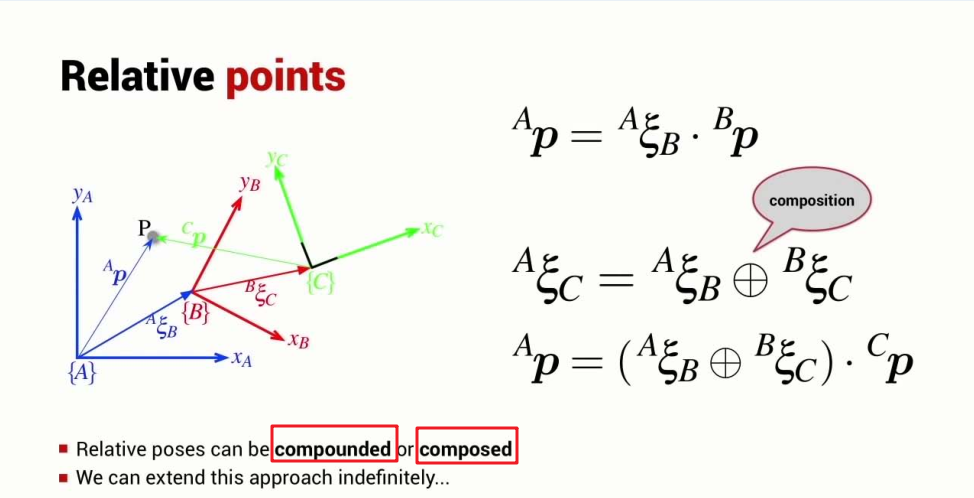

Pose algebra

Describing rotation
How to calculate the rotation?
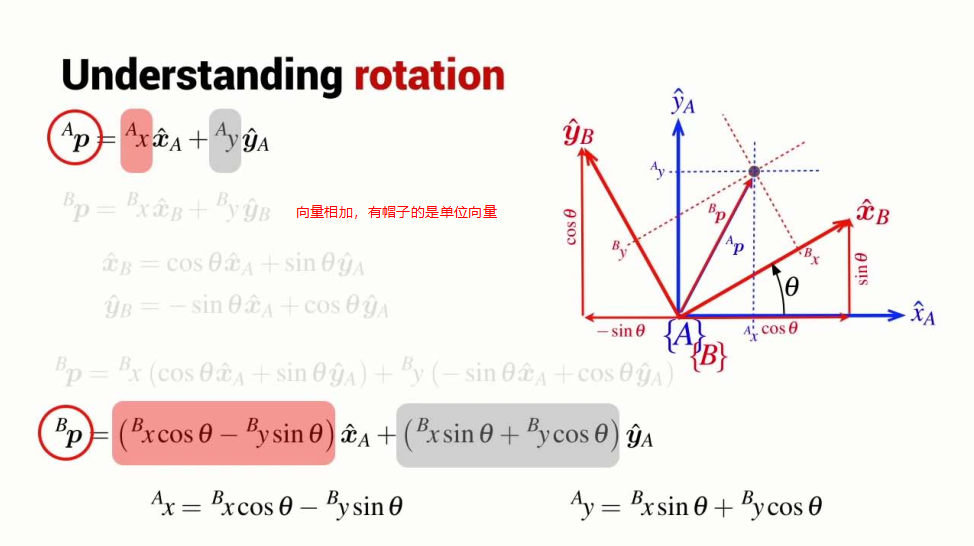
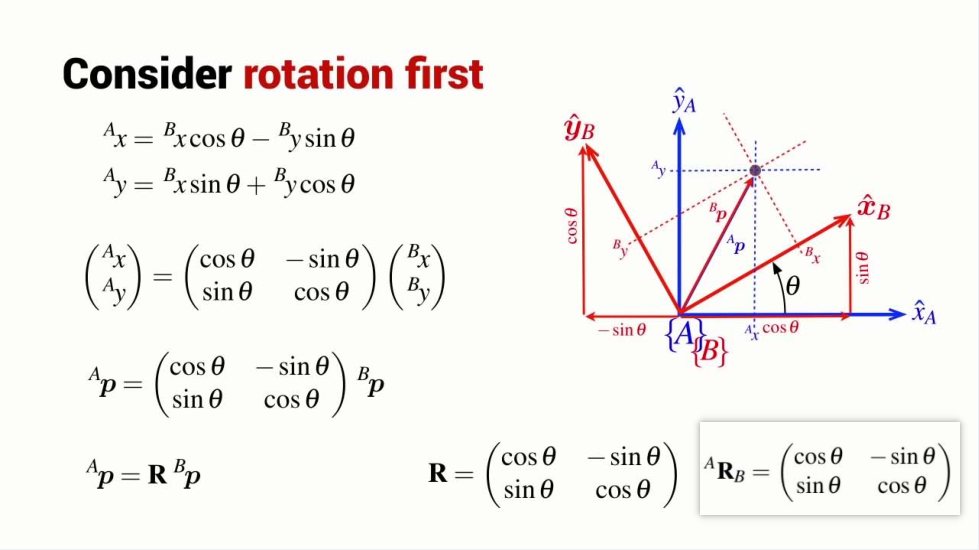
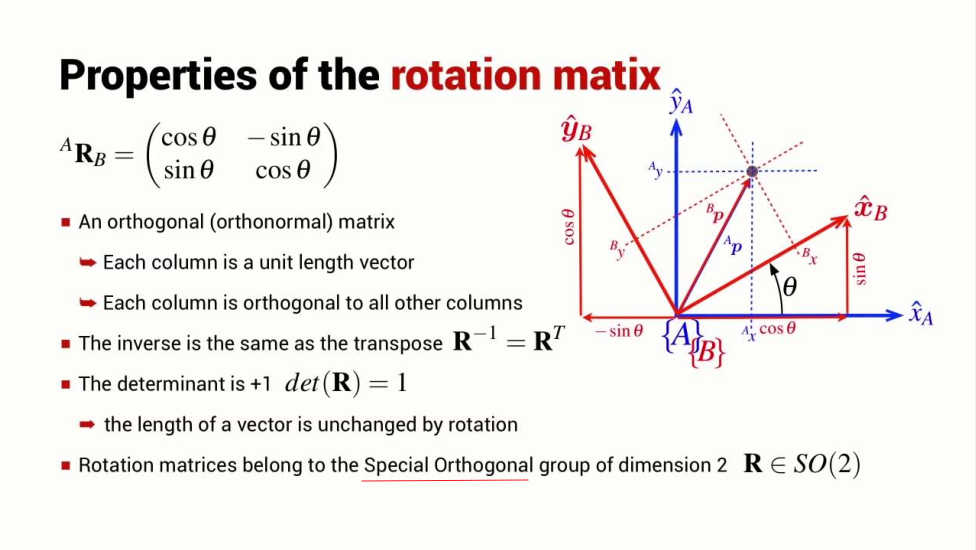
Rotation matix

Describing rotation and translation
- Homogeneous transform



Coding Part
rot2():2 dimensional rotation matrix1
2rot2(0.2)
rot2(30, 'deg')
trot2():homogeneous 2 dimensional rotation matrix1
trot2(30, 'deg')

transl2(): homogeneous transformation representing pure translation1
transl2(x,y)

se2(): homogeneous transform matrix: providing the translation in the x and y directions as well as the angle to be rotated1
se2(x,y,angle,'deg')/se2(x,y,radian)

actually:
se2(x,y,angle,'deg') == transl2(x,y) * trot2(angle,'deg')e2h() && h2e(): function e2h converts Euclid-ean coordinates to homogeneous and h2e performs the inverse conversion;1
$ p1 = h2e(inv(T1) * e2h(P)) % P = [1;2]
More compactly this can be written as
p1 = homtrans( inv(T1), P)
Example1:
pose compounding is not commutative(交换的)1
2
3
4T1 = se2(1,2,30,'deg')
T2 = transl2(2,1) * trot2(0)
T3 = T1 * T2 %This can be thought of the pose 2 with respect to the frame 1
T4 = T2 * T1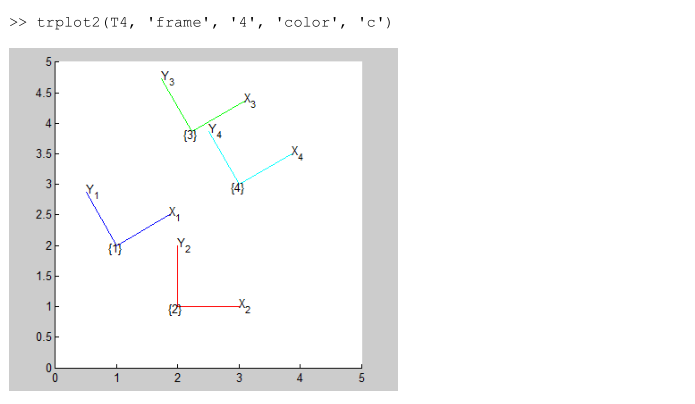
Example2:point with respace to 1
1
2
3p = [3 2]'
plot_point(p)
p1 = inv(T1) * [p;1] % = p1 = inv(T1) * e2h(p)
3DPose
Basic concept
Point && Pose

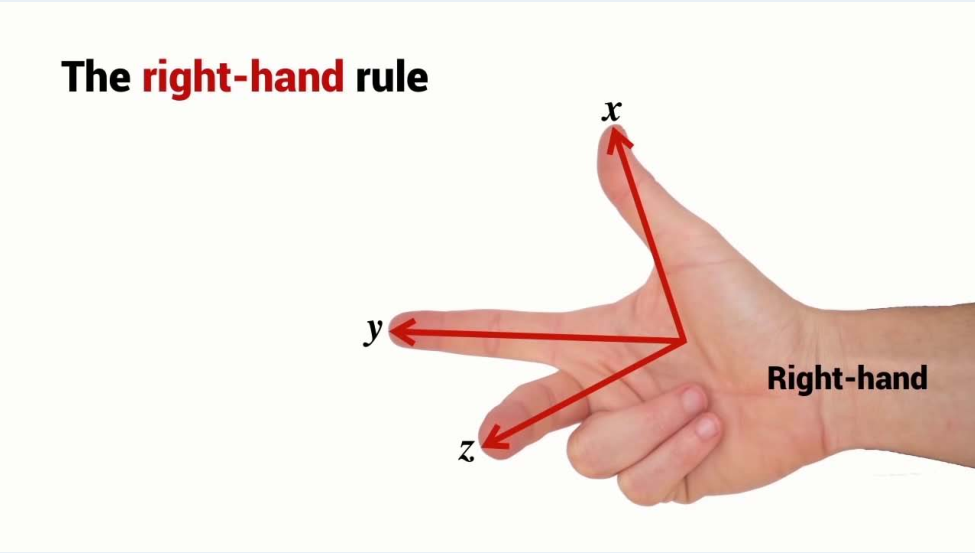
The Right-Hand Rule
Angles increase positively in the anti-clockwise direction
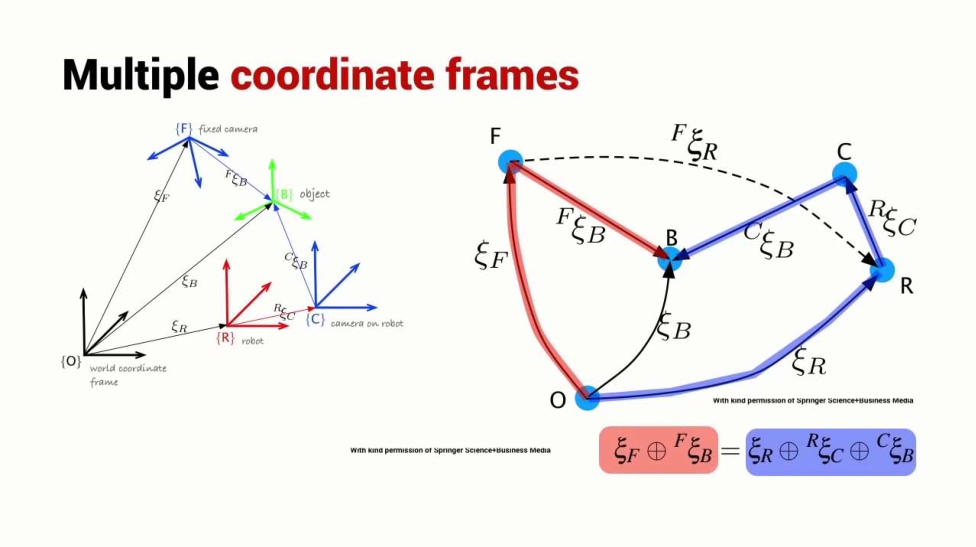
Relative Poses
Relative position/pose

Pose algebra

Representing Orientation in 3-Dimensions
Orthonormal Rotation Matrix
3×3 orthonormal matrix



Coding part
rotx():3 dimensional rotation matrix1
2$ R = rotx(pi/2)
$ R = rotx(45, 'deg')trplot() && tranimate():display a 3d transformation1
2$ trplot(R)
$ tranimate(R)
Three-Angle Representations
Rotation sequences

Euler angles:Euler’s rotation theorem requires successive rotation about three axes such that no two successive rotations are about the same axis.
Representation

Coding:

if θ is negative

if θ=0

Cardan angles/Roll-Pitch-Yaw angles
Representation

Coding

- Fundamental problem:Singularities and Gimbal Lock
This occurs when the rotational axis of the middle term in the sequence becomes parallel to the rotation axis of the first or third term.

Two Vector Representation
- Two Vector Representation

Rotation about an Arbitrary Vector
Any two independent orthonormal coordinate frames can be related by a single rotation about some axis.

Finding the axis;

Coding part:
tr2angvec(R)、eig(R)、angvec2r(pi/2, [1 0 0])


Quaternion
The quaternion is an extension of the complex number – a hyper-complex number – and is written as a scalar plus a vector


Coding part:
Quaternion()is a class


Combining Translation and Orientation
Representing pose
- Pose
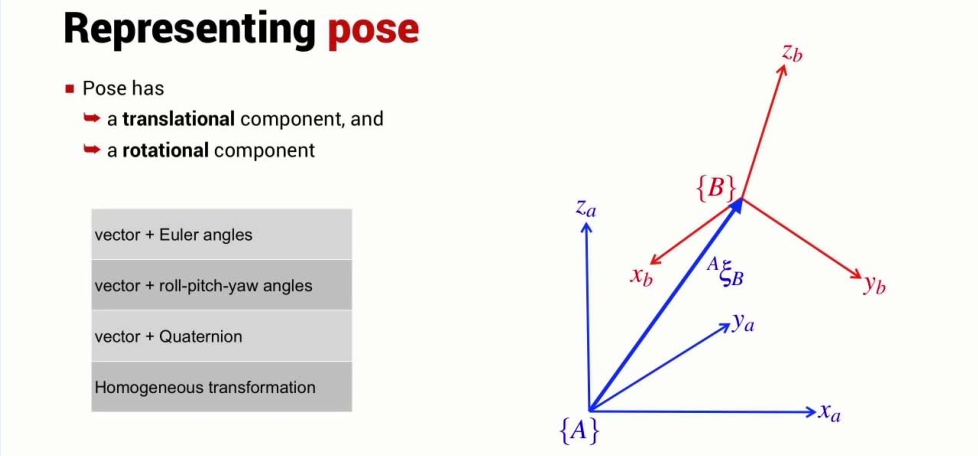
Vecotr-Quaternion
- Vecotr-Quaternion

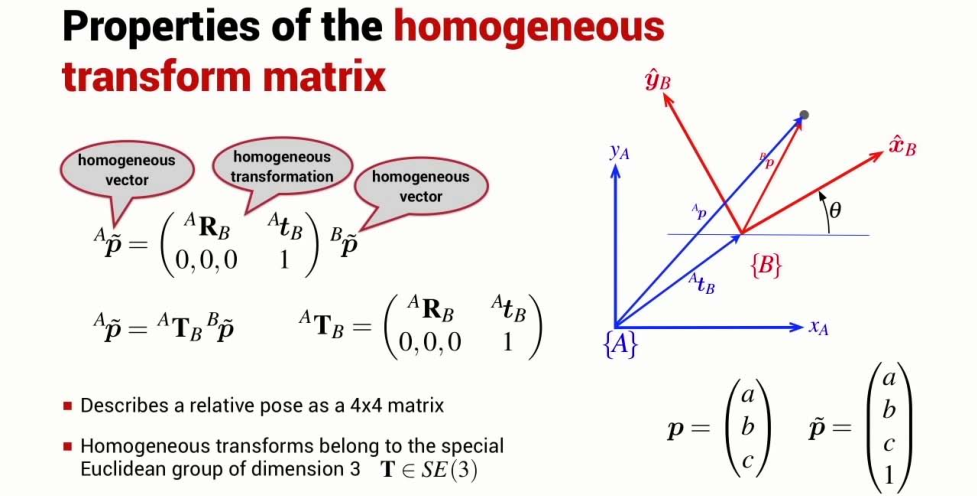
homogeneous transformation matrix
Form

Properties
Coding part:
transl(x,y,z)、trots(pi/20)
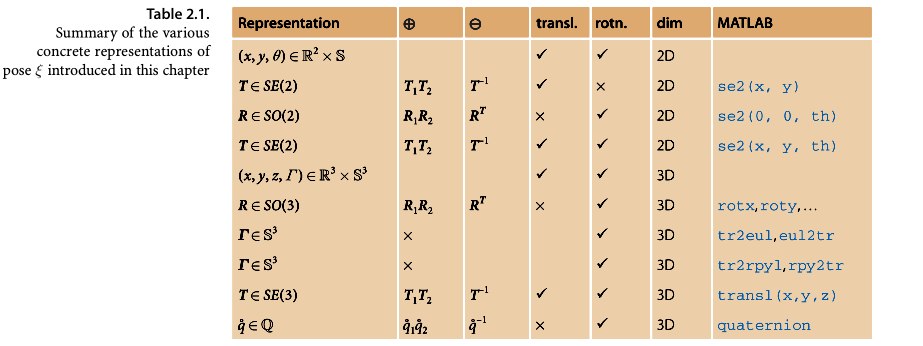
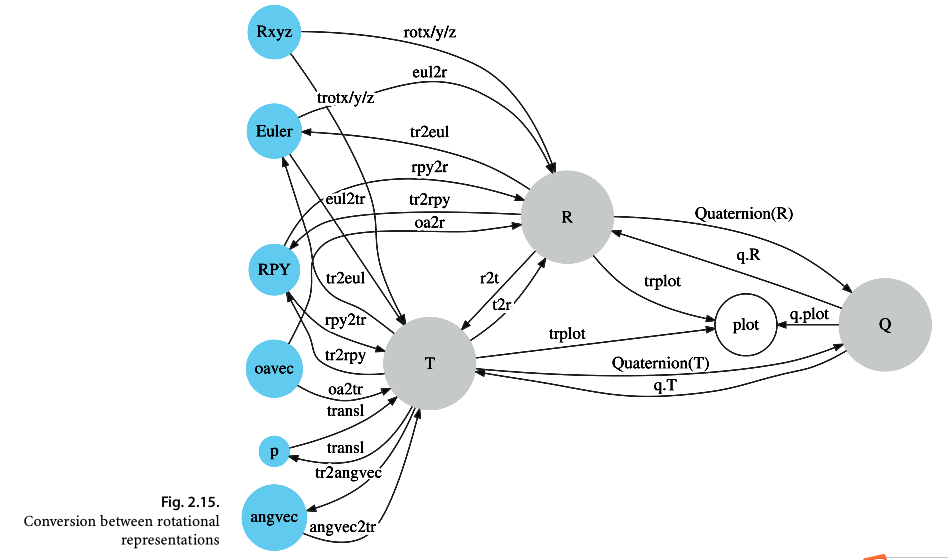
Summary
- Warpping up
Coding part
rotx():3 dimensional rotation matrix1
2$ R = rotx(pi/2)
$ R = rotx(45, 'deg')trplot() && tranimate():display a 3d transformation1
2$ trplot(R)
$ tranimate(R)
Time and Motion
Trajectories
- An important characteristic of a trajectory is that is smooth – position and orientation vary smoothly with time

Smooth One-Dimensional Trajectories
Polynomial function of time


tpoly(): generates a quintic polynomial trajectory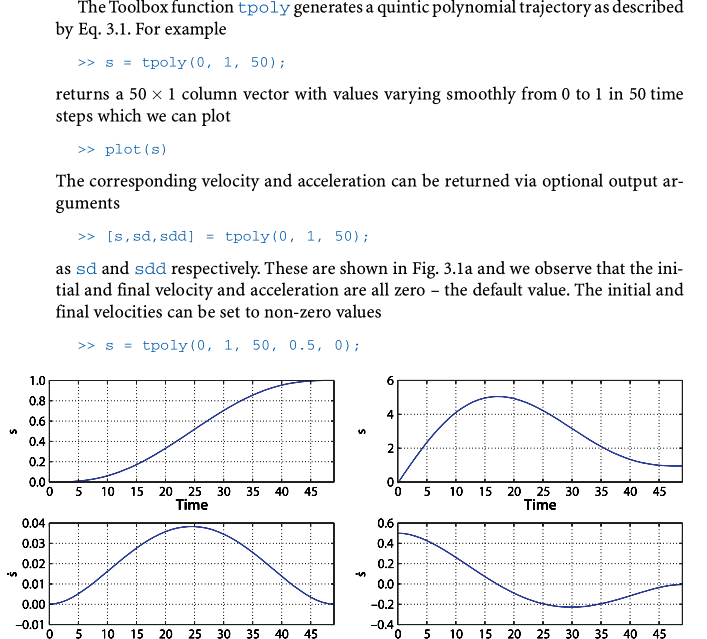

lspb:linear segment (constant velocity) with parabolic blends
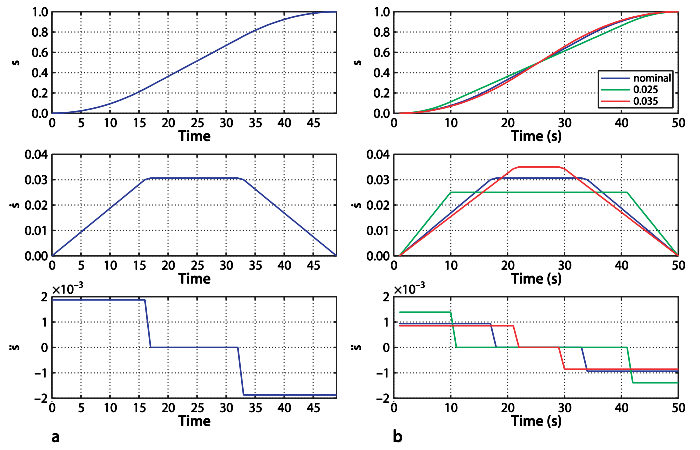
Multi-Dimensional Case
mtraj()/jtraj(): extend the smooth scalar trajectory to the vector case(多维)
Multi-Segment Trajectories
In robotics applications there is often a need to move smoothly along a path through one or more intermediate or via points without stopping. This might be to avoid obstacles in the workplace, or to perform a task that involves following a piecewise continuous trajectory.
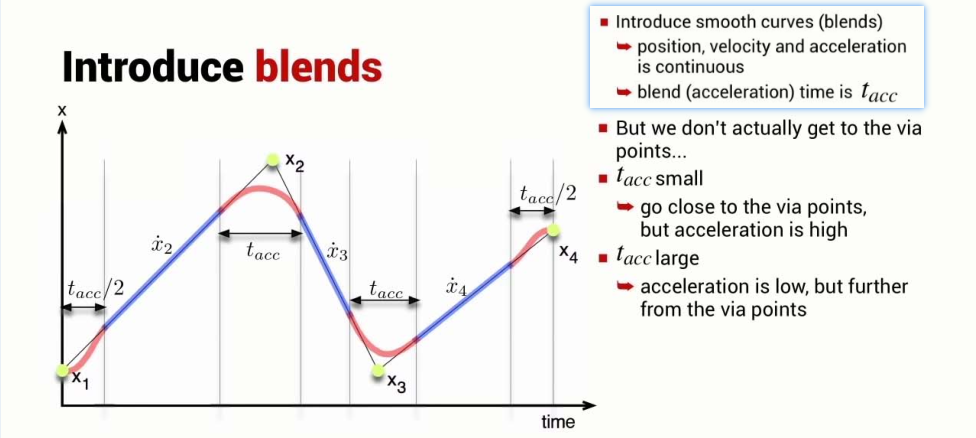
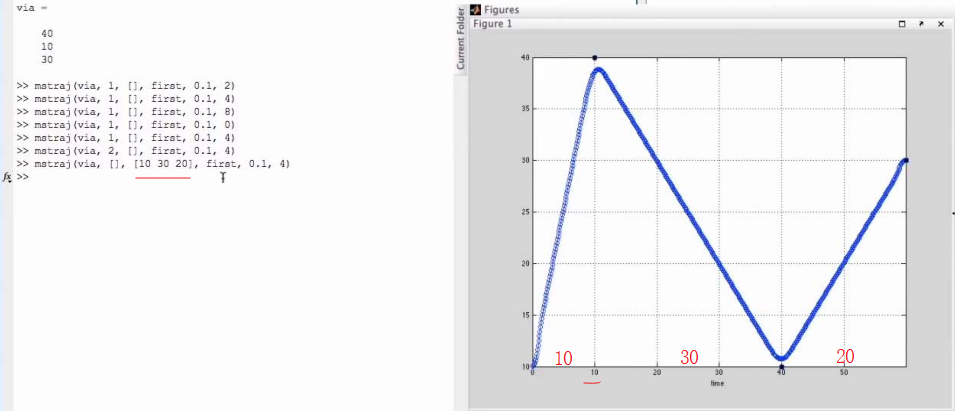
mstraj(): generates a multi-segment multi-axis trajectory based on a matrix of via points
Interpolation of Orientation in 3D
- A rotation matrix must be an orthogonal matrix



- Quaternion interpolation

jtraj()/mtraj(): roll-pitch-yaw angles can be interpolated
interp()

Cartesian Motion
Another common requirement is a smooth path between two poses in SE(3) which involves change in position as well as in orientation. In robotics this is often referred to as Cartesian motion.
- Coding part 2019/4/13 10:36:21 2019/4/13 10:36:24



